Fisica Teorica: Meccanica Statistica
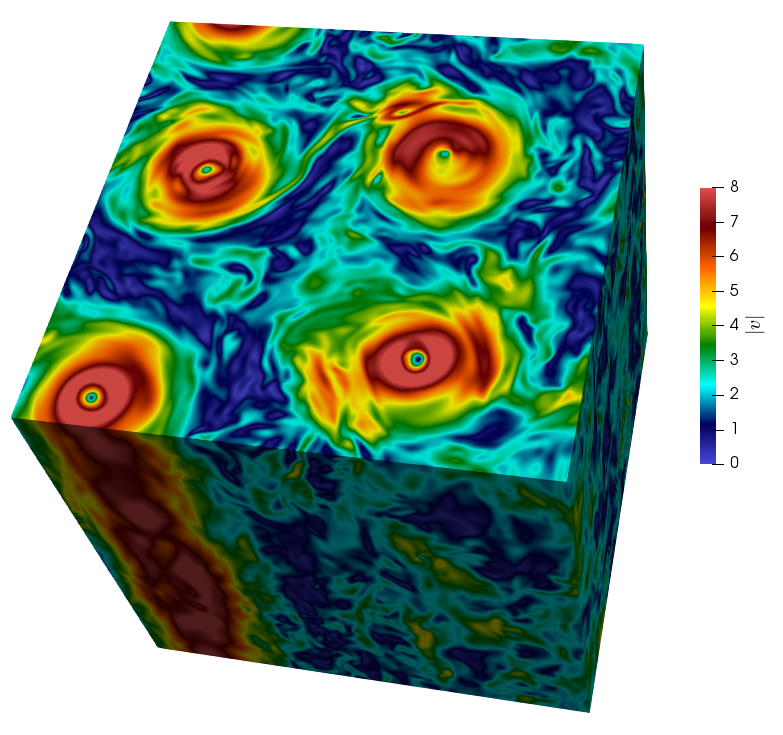
FIG1: Modulo del campo di velocità di un fluido turbolento
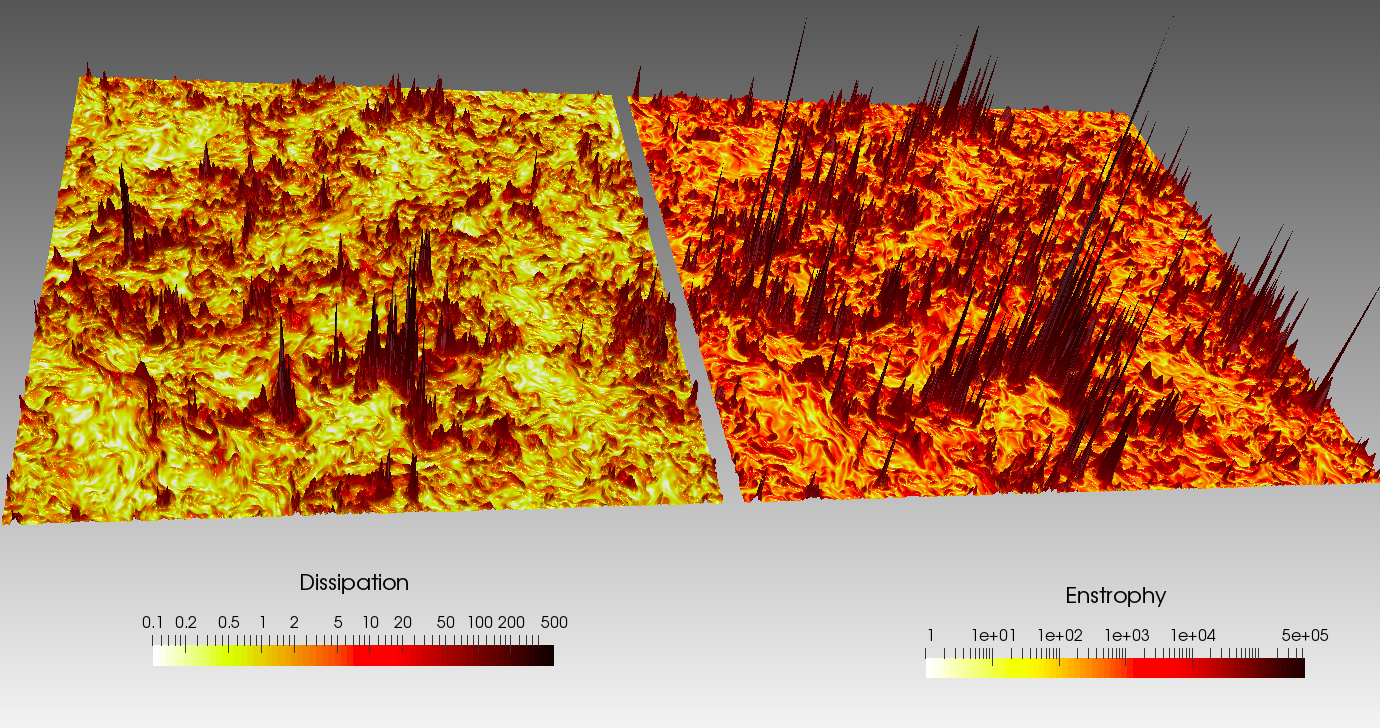
FIG2: Dissipazione di Energia/Enstrofia in fluidi turbolenti

FIG3: Reologia di emulsioni in microcanali strutturati
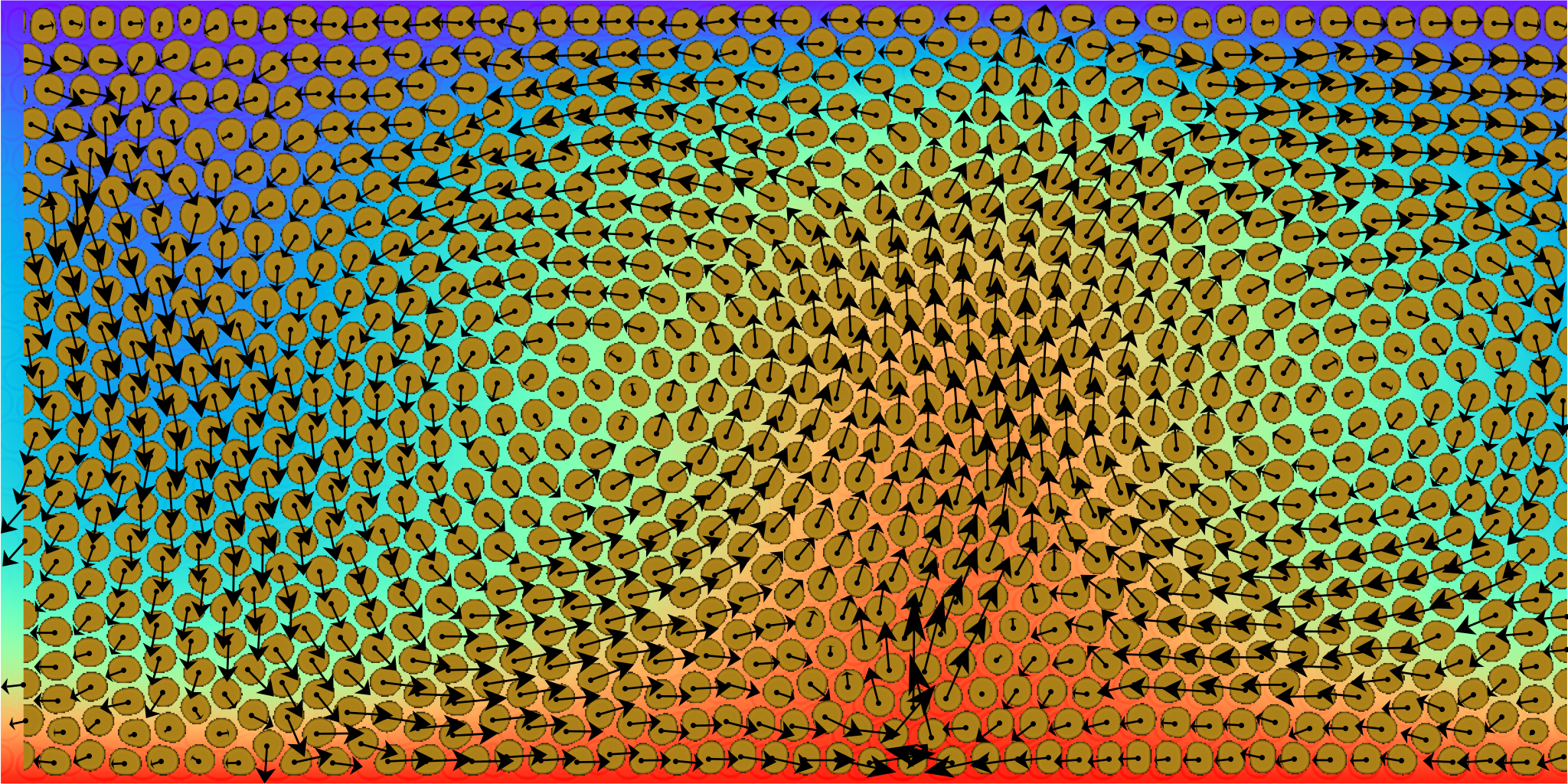
FIG4: convezione in fluidi a più componenti

FIG5: Dinamica di membrane viscoelastiche immerse in fluidi
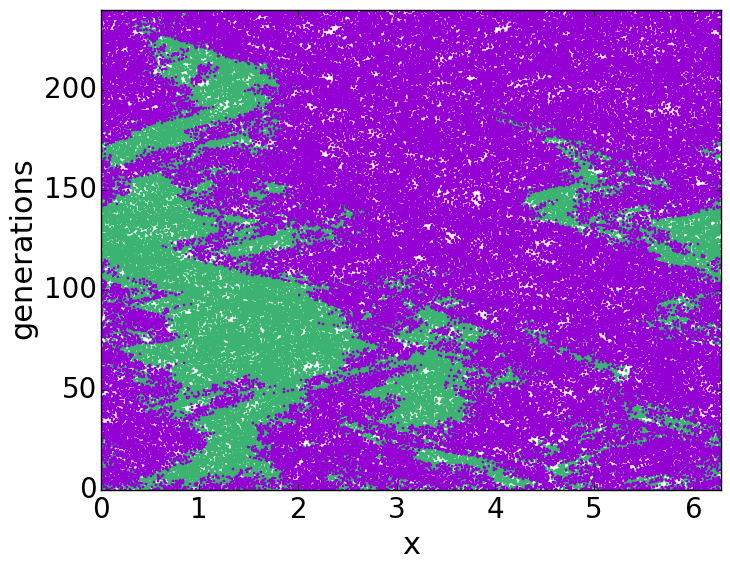
FIG6: Evoluzione spazio-temporale di micro-organismi
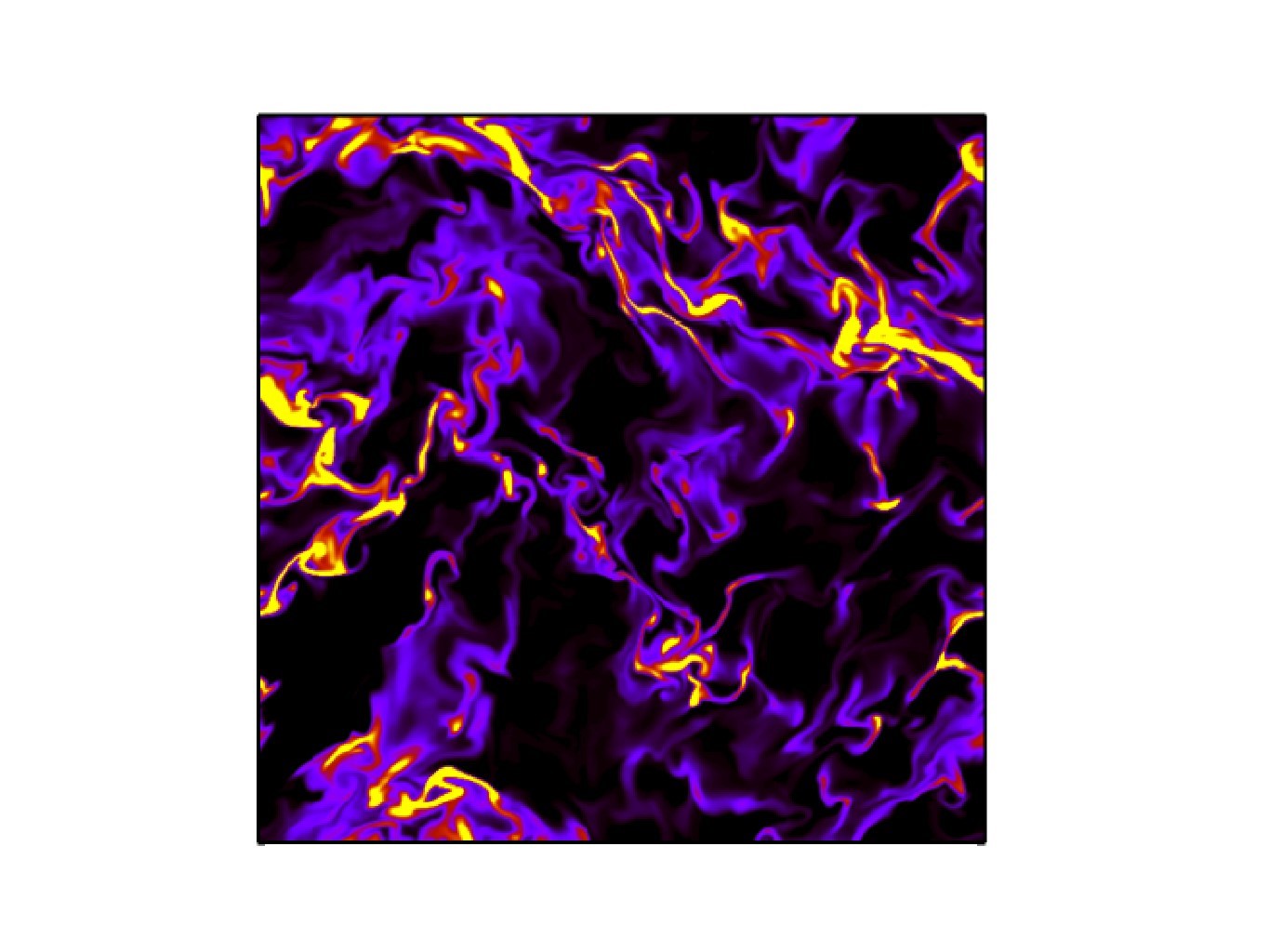
FIG7: Effetti della turbolenza sulla dinamica delle popolazioni
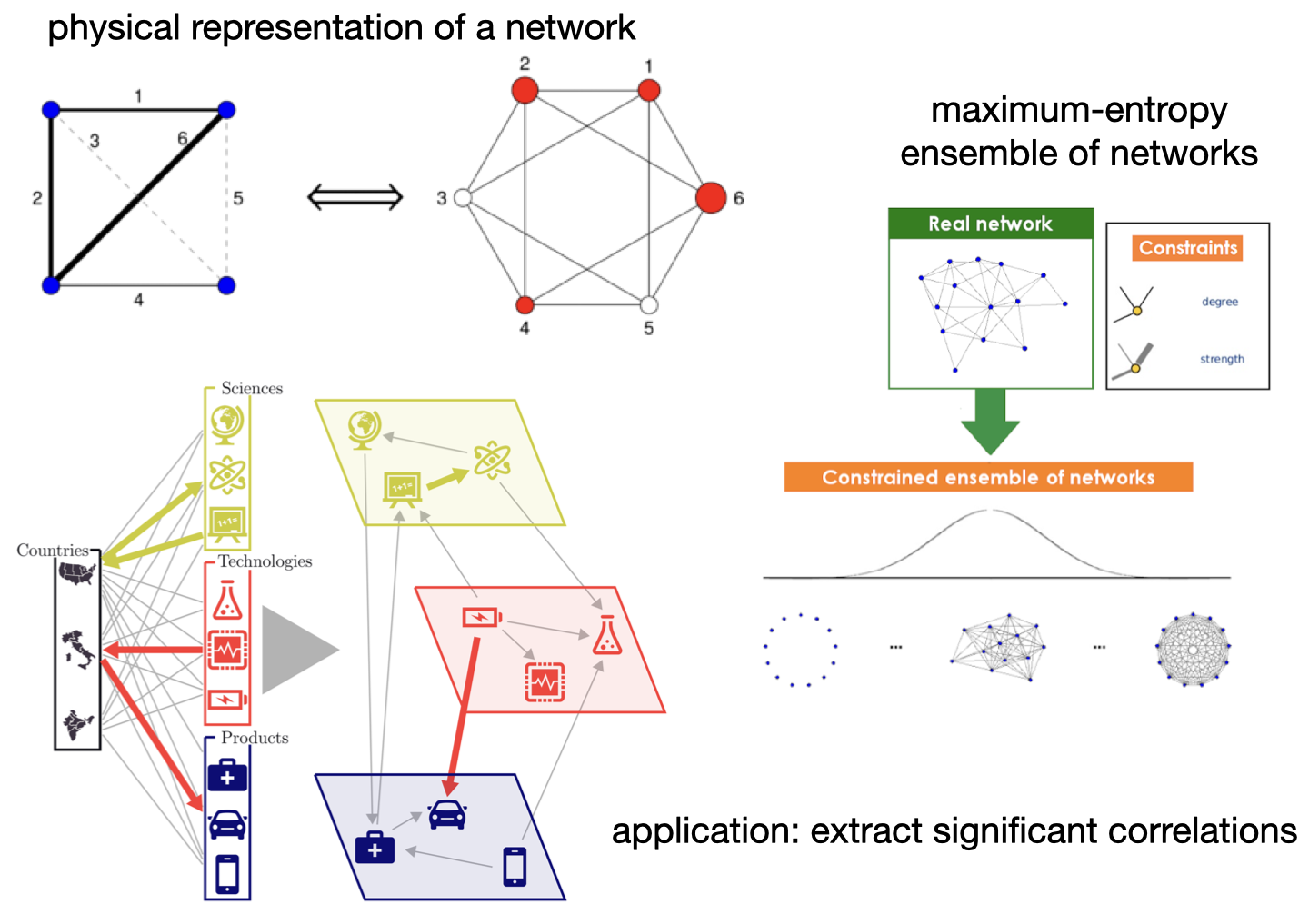
FIG8: Meccanica statistica delle reti con applicazioni
La ricerca riguarda lo studio di fenomeni di meccanica statistica fuori dall’equilibrio, sistemi dinamici e fluidi complessi a differenti scale: dalle piccole scale (fisica cinetica, dinamica delle popolazioni, micro- & nanofluidica) alle grandi scale (dinamica dei fluidi turbolenti), focalizzandosi sia su aspetti fondamentali nel contesto della dinamica dei fluidi, ma anche su aspetti più generali con applicazioni ad ampio spettro (meccanica statistica delle reti e loro applicazioni). La ricerca è condotta con l’ausilio di strumenti teorici matematici e anche computazionali, usando supercomputer presenti nei centri di calcolo europei e in-house.
Personale strutturato (con link alle pubblicazioni):
Fluidi turbolenti: La comprensione del comportamento della dinamica di un fluido turbolento è uno dei problemi più intriganti, frustranti ed importanti della fisica classica (FIG1). E’ un dato di fatto che la maggior parte dei fluidi in movimento abbiano una dinamica complessa il cui ruolo è dominante nella determinazione della fisica del sistema, indipendentemente dalla scala a cui il flusso avvenga. Nonostante il ruolo centrale che i fluidi turbolenti ricoprono nell’universo, la loro dinamica rimane per molti versi indecifrabile. E’ quasi banale ricordare la turbolenza come l’ultimo problema irrisolto della fisica classica. In realtà la turbolenza è molto più di un singolo problema, bensì è un vasto campo di studio con applicazioni centrali nell’ingegneria, nella geofisica, nell’astrofisica fino alla matematica pura. E’ dallo sforzo che negli ultimi decenni i fisici hanno rivolto allo studio della turbolenza che sono nate diverse idee e strumenti tuttora utilizzati in diverse aree della fisica, come il concetto di diffusione anomala (recentemente diventata popolare durante la pandemia di Covid19 a causa della sua importanza nel determinare la propagazione di molecole virali nell’ambiente circostante!) o le leggi di scala a potenza nei problemi a molti-corpi. Importanti nozioni di invarianza di scala e universalità furono per primo proposte nell’ambito della turbolenza. Le principali difficoltà in questo campo, nascono dal fatto che si ha a che fare con un sistema composto da molti gradi di libertà fortemente accoppiati tra loro, fuori dall’equilibrio e in grado di sviluppare fluttuazioni estreme nel campo di velocità.
Il gruppo di ricerca presso il Dipartimento di Fisica di Tor Vergata si occupa ormai da diversi anni dello studio del comportamento di fluidi complessi con approccio sia teorico che numerico, quest’ultimo grazie all’utilizzo dei diversi supercomputer presenti nei centri di calcolo europei e in-house.
Più’ recentemente, una parte delle attività’ di ricerca si sono orientate verso le applicazioni di tecniche di Intelligenza Artificiale come il Machine Learning e il Reinforcement Learning allo studio dei fluidi e flussi complessi. Alcuni dei risultati più prestigiosi hanno permesso di capire come utilizzare delle sonde euleriane (fisse nello spazio) o lagrangiane (che vengono trasportate dal flusso) per ottimizzare e controllare alcune proprietà del fluido, ivi compresa la presenza di eventi estremi nei campi di dissipazione e enstrofia (FIG2). Analogamente, nuove tecniche di big-data e ML si stanno sviluppando per migliorare gli algoritmi di assimilazione dati, necessari nel campo delle meteorologia numerica per sviluppare nuove e piu’ accurate predizioni anche a livello climatologico per il riscaldamento globale.
Personale strutturato coinvolto:
Prof. Luca Biferale, Dr. Michele Buzzicotti, Dr. Fabio Guglietta, Prof. Roberto Benzi
Teoria cinetica (teoria e simulazioni): la teoria cinetica, nell’accezione moderna del termine, indica lo studio di problemi fisici che possono essere descritti da opportune equazioni per funzioni di distribuzione, che danno una descrizione efficace della dinamica di un sistema formato da un gran numero di elementi interagenti. Il prototipo e’ l’equazione di Boltzmann, che descrive lo stato di un gas fuori dall’equilibrio e ha mostrato per la prima volta la connessione con l’idrodinamica.
Questioni fondamentali in meccanica statistica del non-equilibrio sono la derivazione dell’equazione di Boltzmann dalle equazioni di Newton e la derivazione delle equazioni dell' idrodinamica viscosa dall’equazione di Boltzmann. Da un punto di vista matematico, i problemi aperti riguardano l’esistenza di soluzioni dell’equazione di Boltzmann, specialmente in situazioni stazionarie e geometrie generali. Ma la teoria cinetica ha un campo di applicazione piu’ vasto, che spazia da modelli di traffico, a modelli per i mezzi granulari, modelli che descrivono il moto di uccelli (pesci etc), modelli di colloidi, modelli di evoluzione di popolazione e tanti altri altri. Sopratutto negli ultimi anni, nuovi modelli computazionali, noti come ‘Lattice Boltzmann Models’ (LBM) sono stati sviluppati a partire da discretizzazioni spazio-temporali dell’equazione di Boltzmann. Il gruppo di ricerca di Tor Vergata ha dato dei contributi importanti allo sviluppo di LBM, con campi di applicazione tradizionalmente orientati alla comprensione del fenomeno della turbolenza sviluppata. Più recentemente, si sono avuti sviluppi anche verso la simulazione numerica di fluidi complessi a piccole scale (micro- e nanofluidica, FIG3, FIG4) ed in presenza di complessità aggiuntive quali fluttuazioni termiche, coesistenza più fasi/componenti (reologia non-Newtoniana), membrane ed interfacce non ideali (FIG5).
Personale strutturato coinvolto:
Prof. Rossana Marra, Prof. Mauro Sbragaglia, Dr. Fabio Guglietta, Prof. Roberto Benzi
Dinamica delle popolazioni: L’evoluzione dinamica di micro-organismi (o più in generale la "population dynamics" PD) e’ oggetto di ricerca in molti campi scientifici, quali ad esempio biologia, fisica matematica, meccanica statistica. Molti degli esperimenti di laboratorio possono essere compresi (qualitativamente e quantitativamente) in modo soddisfacente. Questo e’ ben lontano dall’essere vero nello studio degli stessi micro-organismi nell’ambiente naturale e in particolare nell’oceano. In questo caso, l’effetto della dinamica turbolenta (incompressibile e/o debolmente compressibile) che trasporta le popolazioni produce una fenomenologia piu’ ricca non ancora compresa (FIG6, FIG7). Effetti legati alle fluttuazioni genetiche possono essere depressi o incrementati a seconda del tipo di turbolenza a cui le popolazioni sono soggette. L’interazione fra la dinamica propria delle popolazioni, inclusi gli effetti delle fluttuazioni genetiche, e la turbolenza e’ il focus di questa linea di ricerca.
Personale strutturato coinvolto:
Meccanica statistica delle reti e applicazioni: le reti complesse sono sistemi caratterizzati da uno schema non banale di interazioni tra le loro unità costitutive, che di solito genera proprietà emergenti come invarianza di scala, mondo piccolo e struttura gerarchico-modulare (FIG8). La fisica delle reti può essere derivata trattando le connessioni stesse come particelle del sistema. In particolare, i modelli di meccanica statistica si derivano dal principio di massima entropia vincolando caratteristiche locali ed eterogenee della rete. Questi modelli possono essere utilizzati in pratica per inferire la rete senza distorsioni in caso di informazioni incompleta, o per rilevare deviazioni significative che possono mettere in luce dettagli importanti del sistema.
Personale strutturato coinvolto: